About the AIOMFAC model

A brief introduction
- What is AIOMFAC?
- Model development
Model details
References

A brief introduction

What is AIOMFAC? ↑Top

The abbreviation AIOMFAC stands for "Aerosol Inorganic-Organic Mixtures Functional groups Activity Coefficients". As this name suggests, AIOMFAC is a thermodynamic model designed for the calculation of activity coefficients of different chemical species in inorganic-organic mixtures – with a focus on those inorganic and organic species known or suggested to be present in atmospheric aerosol particles. The AIOMFAC model is a general thermodynamic activity coefficient model also applicable to other scientific fields.

In the context of chemical thermodynamics activity coefficients are temperature-dependent, component- and mixture-specific parameters describing non-ideal mixing behavior in solutions. Interactions between organic and inorganic mixture components almost always lead to significant deviations from ideal mixing (i.e., deviations from Raoult's law).

The model version available on this website is termed AIOMFAC-web, emphasizing the web-interface and restrictions of this implementation compared to the more general AIOMFAC framework. Specific help and information regarding the use of AIOMFAC-web are given on the Hints & Examples page.

Model development ↑Top

The AIOMFAC model framework and an initial model parameterization for aqueous electrolyte solutions and interactions between inorganic ions and alcohols/polyols at room temperature have been developed by Andreas Zuend (Zünd), Claudia Marcolli, Beiping Luo, and Thomas Peter at ETH Zurich, Switzerland (Zuend et al., 2008). An extension of AIOMFAC to many more organic functional groups and a comprehensive re-parameterization of interaction parameters between inorganic ions and organic functional groups has been realized in subsequent years as part of a collaboration between scientists from the California Institute of Technology (Andreas Zuend, John H. Seinfeld), ETH Zurich (Claudia Marcolli, Thomas Peter, Daniel M. Lienhard, Vacharaporn Soonsin, Ulrich K. Krieger), and the University of Manchester, UK (Alastair M. Booth, David O. Topping, Gordon McFiggans), published in 2011 (Zuend et al., 2011).

The AIOMFAC model has been developed and tested against hundreds of experimental datasets and the model has been shown to be useful, reasonably accurate, and practical for the calculation of activity coefficients in complex multicomponent mixtures as well as for thermodynamic equilibrium computations based on AIOMFAC (vapor-liquid equilibria, solid-liquid equilibria, liquid-liquid equilibria, deliquescence relative humidities, gas-particle partitioning) (Zuend et al. 2008; Zuend et al. 2010; Ciobanu et al. 2010; Zuend et al. 2011; Song et al., 2012; Zuend and Seinfeld, 2012; 2013).

In comparison to other thermodynamic activity coefficient models, AIOMFAC offers several features that most other models lack:

It can be used to calculate activity coefficients of electrolytes, water, and organics from dilute to highly concentrated, supersaturated conditions with respect to crystalline electrolyte phases (i.e., from high to low relative humidity in equilibrium with a liquid solution);
AIOMFAC is one of the very few group-contribution models that can predict non-ideality of organic-inorganic mixtures in a thermodynamically consistent manner (e.g., a requirement for the correct calculation of liquid-liquid phase separation, which is often caused by the salting-out effect of aqueous electrolytes on organic components);
The model offers a wide variety of organic functional groups (allowing thousands of different combinations), seven inorganic cations and five anions, including the sulfuric acid–ammonium bisulfate–ammonium sulfate system.

Model details ↑Top

The AIOMFAC model details are given in the peer-reviewed articles describing the model and its parameterization (Zuend et al., 2008; Zuend et al. 2011). In these papers, a clear description of the thermodynamic basis is presented, including the definition of reference states for molality-based and mole fraction-based activity coefficients and their derivation from expressions of Gibbs excess energy. We encourage people interested in the mathematical expressions and physicochemical basis of AIOMFAC to read the papers. A basic introduction to the thermodynamic principles defining and governing expressions for thermodynamic equilibrium, chemical potentials, and activity coefficients, as well as related consequences such as the Gibbs-Duhem relation and Gibbs' phase rule can be found in advanced textbooks on chemical thermodynamics and are also described in Zuend (2007) and applied in Zuend et al. (2010). An overview of the experimental database used for the parameterization of AIOMFAC is given in the Supplement to the article of Zuend et al. (2011), available here.
In the following paragraphs, some of the important features of AIOMFAC regarding the use and range of applicability of the web-model are introduced.

Gibbs energy contributions: combination of different types of interactions ↑Top

The excess Gibbs energy G^ex characterizes for the overall non-ideality of a thermodynamic system. Different types of interactions involving charged and non-charged (neutral) solution species, interacting over different geometric ranges, can be identified. The total excess Gibbs energy of a multicomponent mixture in the AIOMFAC model is expressed in terms of three contributions from long-range (LR), middle-range (MR) and short-range (SR) interactions between molecules (or functional groups) and ions (Zuend et al., 2008), as shown in Fig. 1. The long-range part, an extended Debye-Hückel expression, and the semi-empirical middle-range part form together a Pitzer-like (group-contribution) model, enabling accurate descriptions of electrolyte solutions, from dilute to highly concentrated (potentially supersaturated) conditions. Short-range interactions between functional groups are calculated with the widely-used UNIFAC model (Fredenslund et al., 1975; Hansen et al. 1991) as modified by Zuend et al. (2011) to include improved specific interaction parameters from Marcolli and Peter (2005) and from Peng et al. (2001).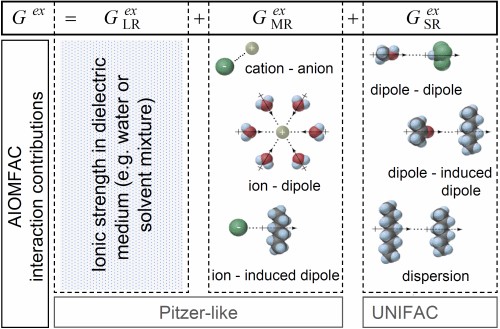
Expressions for activity coefficients of the different species are calculated from the partial derivatives of the Gibbs excess energy at constant temperature and pressure with respect to the molar amounts of the different species in a mixture (see, e.g., Zuend et al., 2011).

Fig. 1: Contributions of different types of interactions to the Gibbs excess energy of a liquid mixture.

Fig. 1. Three major terms represent different types of molecular interactions in a solution and add up to the excess Gibbs energy G^ex of a certain system in the AIOMFAC model. Dispersion forces, also called London forces, are present in any mixture and denote induced dipole-induced dipole interactions. Long-range forces between ions are described by only taking the electric charge interactions into account while neglecting other ion specific properties (e.g. the different radii); this is realized by an extended Debye-Hückel expression. Note that when a group-contribution representation of molecular structures is applied, the different interaction contributions shown here are obtained from the combinations of the partial contributions of different functional groups of a molecule. [Source: Zuend et al., 2008]

Group-contribution concept ↑Top

Since atmospheric aerosols likely contain tens, hundreds, or even thousands of different organic compounds, a practical way to consider this variety of species with a manageable degree of model complexity is by means of organic compound classes and functional groups instead of individual compounds. Therefore, AIOMFAC relies on a group-contribution concept that was introduced with the well-known UNIFAC model (Fredenslund et al. 1975; Hansen et al. 1991), which is also the basis of the LIFAC model (Yan et al. 1999; Kiepe et al. 2006). The LIFAC model and different versions of the UNIFAC model served as a basis for the development of AIOMFAC. In fact, AIOMFAC includes a modified UNIFAC model in addition to a Pitzer-like ion-interaction model and an organic-inorganic mixing term similar to the one in LIFAC, as shown in Fig. 1 above.

The group-contribution concept is based on the idea that physicochemical properties of organic molecules can be represented reasonably well by segmenting a molecule into different "functional" groups and consideration of specific properties of these functional groups. This leads to the description of a liquid mixture as a "solution of groups" (instead of a solution of molecules, see also Fig. 3 below). This concept has been proven useful; it is often a good approximation for the real behavior of organic mixtures and aqueous organic mixtures (see references to UNIFAC and mod. UNIFAC models). However, there are also limitations to a group-contribution approach as discussed in Zuend et al. (2011), e.g., when applied to complex, multifunctional organic compounds, effects of intramolecular interactions between functional groups in close proximity are usually not considered. Such intramolecular effects can be considered only by introducing additional types of functional groups or second order correction coefficients, which is often not a viable approach as it would further complicate the approach instead of keeping it as simple as possible.

Main groups and subgroups ↑Top

AIOMFAC and UNIFAC distinguish between two levels of functional group classification: main groups and subgroups. Main groups comprise a less resolved classification of functional groups ignoring the number of hydrogen atoms bonded to carbon atoms, e.g., CH_n (alkyl main group), or CH_nCO (ketone main group). Subgroups further differentiate between groups of the same main group consisting of different numbers of H-atoms, e.g., between CH₃, CH₂, CH, and C of the same (standard) alkyl main group or between the subgroups CH₃CO and CH₂CO of the ketone main group. The AIOMFAC main groups and examples of their assignments to organic structures are shown in Fig. 2.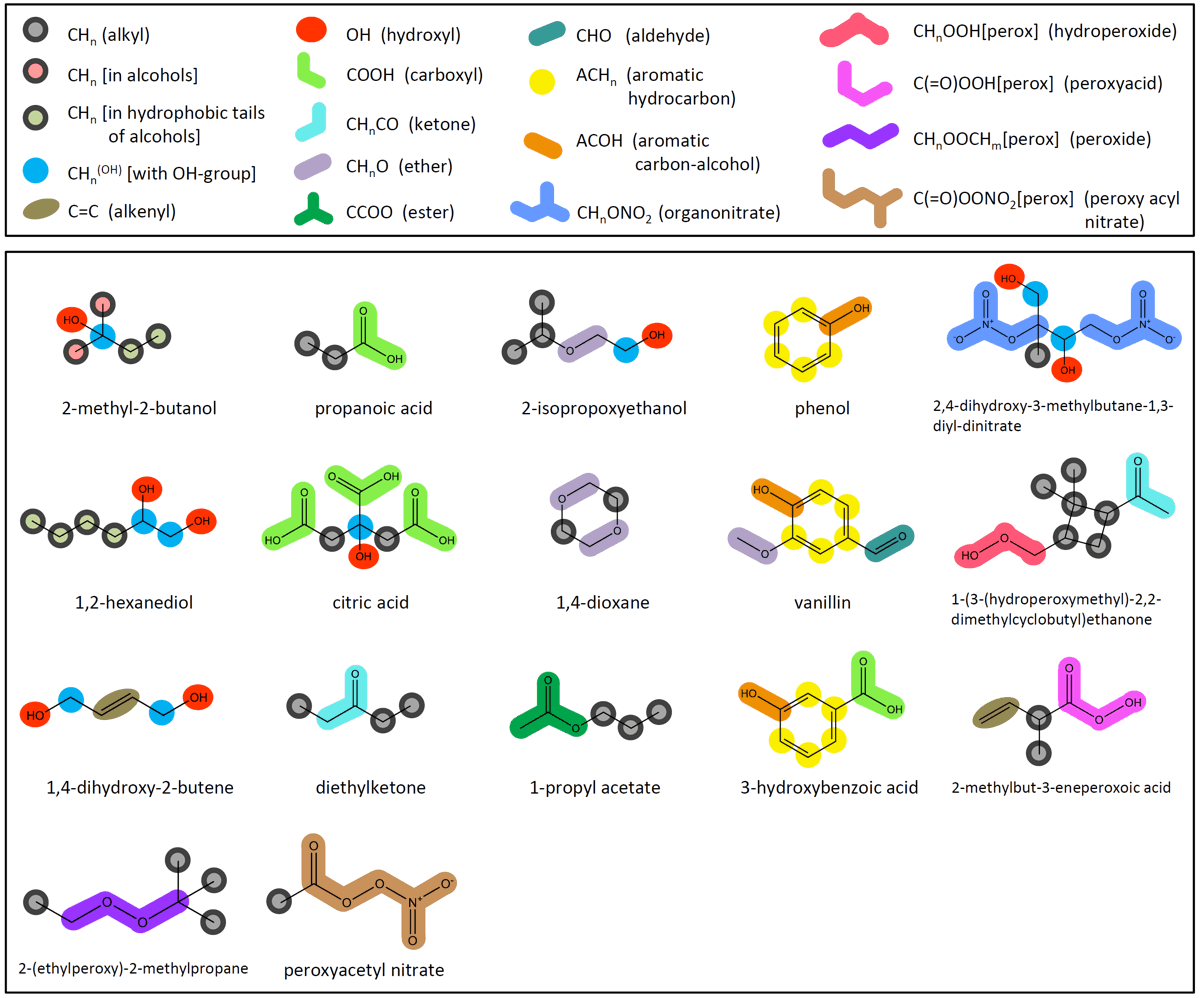

Fig. 2: AIOMFAC main groups and examples of assignments.

Fig. 2. Upper box: complete list of types of organic functional main groups used in AIOMFAC. Besides the functional groups and associated interaction parameters of standard UNIFAC (Hansen et al., 1991), specific groups of Peng et al. (2001) (carboxyl) and of Marcolli and Peter (2005) are used, leading to a distinction between different alkyl groups (as shown in the examples). AIOMFAC middle-range main group ↔ ion interactions involving the specific alkyl groups CH_n^[alc–tail] [in hydrophobic tails of alcohols] and CH_n^[alc] [in alcohols, (but not in hydrophobic tail nor bonded to OH group)] are described with the same parameters as CH_n (standard UNIFAC) ↔ ion interactions, denoted by the common outline color of the alkyl groups. UNIFAC parameters for the groups: hydroperoxide, peroxyacid, peroxide, peroxyacyl nitrate, and organonitrate are taken from Compernolle et al. (2009).
Lower box: examples of main group assignments to molecular structures. [Source: adapted from Zuend et al., 2011]

Main groups of organic compounds are used to describe middle-range interactions between dissolved inorganic ions and functional groups, as the number of H-atoms bonded to C-atoms plays a minor role compared to the polarity of carbon-oxygen bonds. That is, organic compounds are still treated as a combination of subgroups, but the activity coefficient contributions from different subgroups of a certain main group interacting with ions are assigned the same value (the main group interaction value). However, in the UNIFAC short-range part of AIOMFAC, interactions between organic functional groups and their interactions with water molecules (main group = subgroup = H₂O) are resolved on the subgroup level. Therefore, in the input to AIOMFAC, the organic compounds need to be defined in terms of subgroups (main groups are then assigned automatically based on the stated subgroups). An example of the segmentation of an organic substance (ferulic acid) in terms of subgroups and their mixing with water and a salt (here NaCl) as a solution of groups is shown in Fig. 3.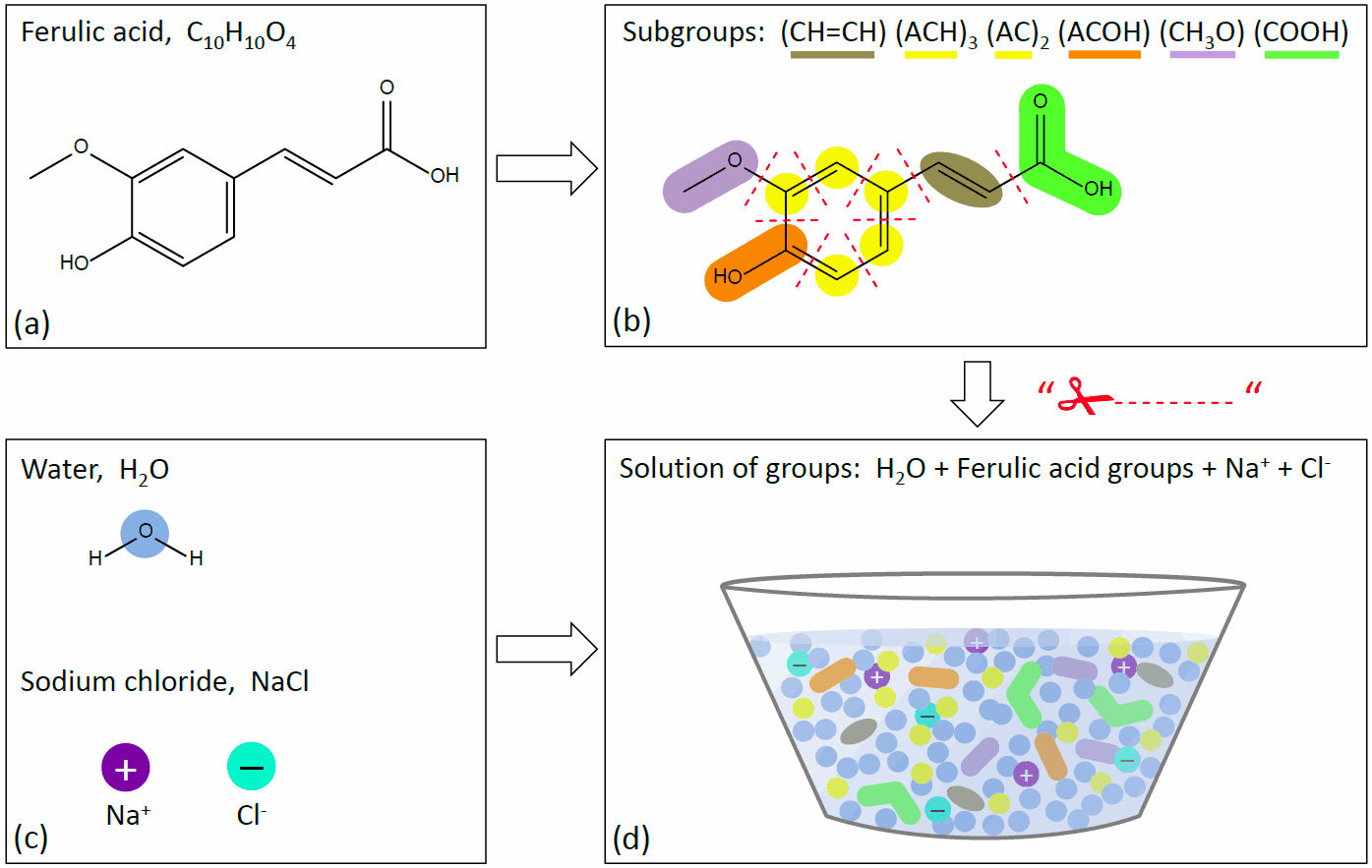

Fig. 3: Sketch of AIOMFAC subgroup assignments and solution of group mixing.

Fig. 3. Sketch of AIOMFAC subgroup assignments and mixture representation as a "solution of groups" using the example of the system ferulic acid + water + NaCl. (a) Chemical structure of a ferulic acid molecule. (b) Segmentation of the organic species into different subgroups (colored by main groups as in Fig. 2). The dashed red lines indicate where the molecular structure is "cut" to end up with individual groups in the solution-of-groups representation of panel (d). (c) Water and inorganic ions are represented as single groups (main group = subgroup). (d) Organic-inorganic mixture of the different system components as a solution of groups. Of course, in reality the molecular structures are not lost in solution, but the representation in (d) indicates that a group-contribution model like AIOMFAC does not (need to) know which subgroups belong to which compound. AIOMFAC calculates activity coefficients for each individual subgroup in this mixture as a function of the composition and temperature (temperature range is restricted to room temperature, ~298 K, in the presence of inorganic ions). To obtain the activity coefficient of a whole organic molecule, the partial contributions of the different subgroups are combined again according to their stoichiometric abundance in the molecule, i.e., following steps (d) → (b) → (a) back to the molecular compounds. [Source: figure by A. Zuend]

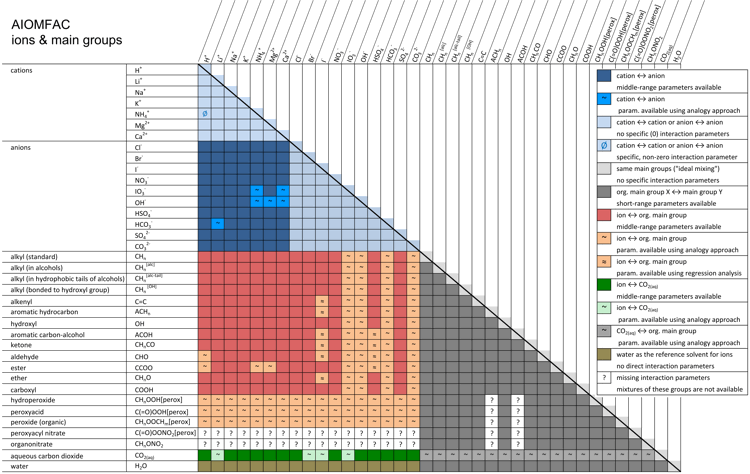
The procedure for the definition of mixtures other than the one shown in Fig. 3, including systems containing multiple organic and inorganic substances, follows the same basic steps. While the number of different main groups and subgroups remain limited and manageable, the number of organic species which can be represented by AIOMFAC subgroups is, in principle, unlimited. Hence, adding hundreds of different species to a mixture for a specific AIOMFAC calculation only seems to make the system more complex, yet most of the organic components will share some (or all) of their subgroups with the pool of subgroups already present due to the definition of other system components. Adding compounds consisting of subgroups already present in the mixture will therefore change only the relative abundance (mole fractions) of subgroups, but not the complexity of the system as seen by AIOMFAC. Thus, as a limiting case, the solution-of-groups representation cannot become more complex than the maximum number of different subgroups available in AIOMFAC (currently ~40 organic subgroups (13 main groups), 12 ions, and water). This reduced complexity is one of the aspects that make the group-contribution concept a powerful and practical method. Another advantage of the group-contribution concept is its predictive capability: it can be used to predict properties of molecular structures that have not been measured or modeled before. This is important with regard to predictions of activity coefficients and pure compound vapor pressures of organic compounds in the atmosphere.

Chemical species ↑Top

As described above, the list of chemical species available for calculations with AIOMFAC is enormous. Possible organic compounds are only limited by the types of organic functional groups currently available in AIOMFAC. AIOMFAC essentially comprises the whole list of organic functional groups available in standard UNIFAC (see Hansen et al., 1991), but since the focus of AIOMFAC is on organic-inorganic mixtures, only organic main groups for which also middle-range interaction parameters with inorganic ions have been determined are made available in AIOMFAC-web (with a few exceptions). Figure 4 shows the list of cations, anions, and organic main groups currently available. If a main group is available, all pertaining subgroups are available too – and these can be selected from the drop-down lists on the model input page (Run Model). Missing interaction parameters are indicated by a question mark in Fig. 4. Missing parameters could be the cause of an error message from AIOMFAC-web in case a mixture that would require undetermined parameters had been defined as model input. The reason for missing interaction parameters is the lack of experimental data required to determine corresponding AIOMFAC model parameters. In some cases, missing model parameters can be estimated based on an analogy approach as described in Zuend and Seinfeld (2012) using the functional group polarity series of Zuend et al. (2011) as constraints.

Fig. 4. AIOMFAC group interaction matrix indicating available and missing binary interaction parameters. Colored entries show different kinds of specific group ↔ group interactions implemented in the model. As indicated, some of the interaction parameters have been estimated based on an analogy approach (Zuend and Seinfeld, 2012) or a regression method (Yin et al., 2022) rather than by direct determination from an AIOMFAC model fit to experimental data (due to insufficient measurements). White cells marked with a "?" indicate missing interaction parameters. AIOMFAC-web can perform computations only for systems for which all required binary interactions are covered in this matrix. Click here to display a larger version of this figure. [Source: figure by A. Zuend with adaptation and updates by Yin et al. (2022)]

Temperature range ↑Top

The valid temperature range covered by AIOMFAC depends on the type of a mixture activity coefficients are computed for. In case of aqueous electrolyte solutions and (aqueous) mixtures of organic components and electrolytes, the temperature range is limited to room temperature, in a strict sense to 298.15 K (25 °C). However, activity coefficients are rather weak functions of temperature (Gibbs-Helmholtz equation), e.g., in contrast to vapor pressures. Therefore, AIOMFAC calculations in a temperature range close to 298 K, say ±10 K, will be applicable. In many cases a larger deviation (±20 K, ±30 K) from 298 K will still provide a good estimate for activity coefficients in organic-inorganic mixtures, as the AIOMFAC model has been parameterized using also experimental data deviating from 298 K and the model contains several terms which at least to some extent account for a temperature effect (likely better constrained towards temperatures higher than 298 K). The rather weak temperature dependence of activity coefficients should not be confused with the temperature dependence of solubility limits of organic compounds and inorganic salts or the temperature dependence of dissociation constants, because equilibrium "constants" have also a temperature dependence on their own.

The temperature dependence of electrolyte-free mixtures (aqueous organic solutions) is described over a wider range of temperatures, since in this case AIOMFAC reduces to a modified UNIFAC model, including the relatively simple temperature dependent main group interaction parameterization of standard UNIFAC. In this case, the valid / applicable temperature range is ~280 K to ~400 K. Note that there are modified versions like UNIFAC Dortmund, which allow a physically better and more reliable description of temperature dependency. In all cases AIOMFAC will likely perform better at temperatures higher than room temperature as compared to similar deviations to lower temperatures, because the experimental database used to determine interaction parameters was biased towards more data at higher temperatures. An improved description of the temperature dependence of activity coefficients will be made available in a future version of AIOMFAC.

References ↑Top

↑ back to text

Ciobanu, V. G., Marcolli, C., Krieger, U. K., Zuend, A., and Peter, T.: Efflorescence of ammonium sulfate and coated ammonium sulfate particles: evidence for surface nucleation., J. Phys. Chem. A, 114, 9486–9495, doi:10.1021/jp103541w, http://dx.doi.org/10.1021/jp103541w, 2010.
Compernolle, S., Ceulemans, K., and Müller, J.-F.: Influence of non-ideality on condensation to aerosol, Atmos. Chem. Phys., 9, 1325–1337, doi:10.5194/acp-9-1325-2009, http://www.atmos-chem-phys.net/9/1325/2009/, 2009.
DeRieux, W.-S. W., Li, Y., Lin, P., Laskin, J., Laskin, A., Bertram, A. K., Nizkorodov, S. A., and Shiraiwa, M.: Predicting the glass transition temperature and viscosity of secondary organic material using molecular composition, Atmos. Chem. Phys., 18, 6331–6351, https://doi.org/10.5194/acp-18-6331-2018, 2018.
Fredenslund, A., Jones, R. L., and Prausnitz, J. M.: Group-Contribution Estimation of Activity Coefficients in Nonideal Liquid Mixtures, AIChE J., 21, 1086–1099, 1975.
Gervasi, N. R., Topping, D. O., and Zuend, A.: A predictive group-contribution model for the viscosity of aqueous organic aerosol, Atmos. Chem. Phys., 20, 2987–3008, https://doi.org/10.5194/acp-20-2987-2020, 2020.
Hansen, H. K., Rasmussen, P., Fredenslund, A., Schiller, M., and Gmehling, J.: Vapor-liquid-equilibria by UNIFAC group contribution. 5. Revision and extension, Ind. Eng. Chem. Res., 30, 2352–2355, 1991.
Kiepe, J., Noll, O., and Gmehling, J.: Modified LIQUAC and modified LIFAC – A further development of electrolyte models for the reliable prediction of phase equilibria with strong electrolytes, Ind. Eng. Chem. Res., 45, 2361–2373, doi:10.1021/ie0510122, 2006.
Lilek, J. and Zuend, A.: A predictive viscosity model for aqueous electrolytes and mixed organic–inorganic aerosol phases, Atmos. Chem. Phys., 22, 3203–3233, https://doi.org/10.5194/acp-22-3203-2022, 2022.
Marcolli, C. and Peter, Th.: Water activity in polyol/water systems: new UNIFAC parameterization, Atmos. Chem. Phys., 5, 1545–1555, doi:10.5194/acp-5-1545-2005, http://www.atmos-chem-phys.net/5/1545/2005/ 2005.
Peng, C., Chan, M. N., and Chan, C. K.: The hygroscopic properties of dicarboxylic and multifunctional acids: Measurements and UNIFAC predictions, Environ. Sci. Technol., 35, 4495–4501, doi:10.1021/es0107531, http://dx.doi.org/10.1021/es0107531 2001.
Song, M., Marcolli, C., Krieger, U. K., Zuend, A., and Peter, T.: Liquid-liquid phase separation and morphology of internally mixed dicarboxylic acids/ammonium sulfate/water particles, Atmos. Chem. Phys., 12, 2691-2712, doi:10.5194/acp-12-2691-2012, http://www.atmos-chem-phys.net/12/2691/2012/, 2012.
Yan, W. D., Topphoff, M., Rose, C., and Gmehling, J.: Prediction of vapor-liquid equilibria in mixed-solvent electrolyte systems using the group contribution concept, Fluid Phase Equilib., 162, 97–113, 1999.
Yin, H., Dou, J., Klein, L., Krieger, U. K., Bain, A., Wallace, B. J., Preston, T. C., and Zuend, A.: Extension of the AIOMFAC model by iodine and carbonate species: applications for aerosol acidity and cloud droplet activation, Atmos. Chem. Phys., 22, 973–1013, https://doi.org/10.5194/acp-22-973-2022, 2022.
Zuend, A.: Modelling the Thermodynamics of Mixed Organic-Inorganic Aerosols to Predict Water Activities and Phase Separations, Phd thesis, ETH Zurich, Zurich, Switzerland, doi:10.3929/ethz-a-005582922, http://e-collection.ethbib.ethz.ch/view/eth:30457, 2007.
Zuend, A. and Seinfeld, J. H.: Modeling the gas-particle partitioning of secondary organic aerosol: the importance of liquid-liquid phase separation, Atmos. Chem. Phys., 12, 3857–3882, doi:10.5194/acp-12-3857-2012, http://www.atmos-chem-phys.net/12/3857/2012/, 2012.
Zuend, A. and Seinfeld, J. H.: A practical method for the calculation of liquid–liquid equilibria in multicomponent organic–water–electrolyte systems using physicochemical constraints, Fluid Phase Equilib., 337, 201–213, doi:10.1016/j.fluid.2012.09.034, http://dx.doi.org/10.1016/j.fluid.2012.09.034, 2013.
Zuend, A., Marcolli, C., Luo, B. P., and Peter, T.: A thermodynamic model of mixed organic-inorganic aerosols to predict activity coefficients, Atmos. Chem. Phys., 8, 4559–4593, doi:10.5194/acp-8-4559-2008, http://www.atmos-chem-phys.net/8/4559/2008/, 2008.
Zuend, A., Marcolli, C., Peter, T., and Seinfeld, J. H.: Computation of liquid-liquid equilibria and phase stabilities: implications for RH-dependent gas/particle partitioning of organic-inorganic aerosols, Atmos. Chem. Phys., 10, 7795–7820, doi:10.5194/acp-10-7795-2010, http://www.atmos-chem-phys.net/10/7795/2010/, 2010.
Zuend, A., Marcolli, C., Booth, A. M., Lienhard, D. M., Soonsin, V., Krieger, U. K., Topping, D. O., McFiggans, G., Peter, T., and Seinfeld, J. H.: New and extended parameterization of the thermodynamic model AIOMFAC: calculation of activity coefficients for organic-inorganic mixtures containing carboxyl, hydroxyl, carbonyl, ether, ester, alkenyl, alkyl, and aromatic functional groups, Atmos. Chem. Phys., 11, 9155–9206, doi:10.5194/acp-11-9155-2011, http://www.atmos-chem-phys.net/11/9155/2011/, 2011.